
| Calculation |  |
| Quality Mathematics in the mid-18th Century | Click on any image for a larger view. Scroll to view more items. |
 |
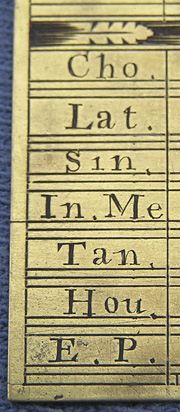 |
 |
 |
|
FINELY CRAFTED RULE BY FRANCIS WATKINS, English, mid 18th century, signed "F. Watkins, London," of thin brass 6-1/4" x 1-3/4" (16 x 4.5 cm) decorated both sides with running leaf tip design. The front has gently beveled edges, and is exquisitely engraved with a rectangular protractor (divided every half-degree) and with scales of equal parts with transversals for interpolation. The reverse has further chart scales, and complex scales for calculation (Cho, Lat, Sin, In Me, Tan, Hou, E P, Rum, Lon, Sec, Sec Continued, and Tan Continued). Very fine condition. (8606) $2400. |
| Public Permitted to Telegraph Coded Phrases! | Click on any image for a larger view. Scroll to view more items. |
 |
 |
 |
|
SITTLER'S CODE BOOK, French, published 1885, entitled Dictionnaire Abréviatif Chiffré. Bound in maroon fabric, 4-3/4" x 7-3/4" (12 x 20 cm), the book has 100 pages, each with 100 numbered words and phrases arranged alphabetically throughout, plus three pages of instructions, enabling "Correspondence Secrète." Condition is good, the last few pages coming loose. This "7th edition" explains that all editions are the same, also that a French law of 13 June 1866 permitted the public to correspond by telegraph using number codes. In use you and your recipient need copies of the book, and you must both identically hand-number the pages in any order from 00 to 99. Identifying each word or phrase by the numbered page followed by its numbered entry, thus by a four-digit number, we can generate a message as follows, using our particular book: 1131 = Avez-vous acheter; 5822 = Instrument; 1420 = Anglais; and thus "Have you bought the English instrument ?" (10405) $195. |
| With a Myriad of Scales for Chart and Map Making | Click on any image for a larger view. Scroll to view more items. |
 |
|
THE GUNTER "RECONNAISSANCE PROTRACTOR," English, c. early 20th century, stamped with the signature of Edward Gunter, Lt. Col., registered #270665. The 6" (15 cm) long boxwood rule has beveled edges to the front, and is stamped both sides with a wealth of scales and equations for chart and map making, especially in surveying. Included are a rectangular protractor, linear reduction scales including with transversals, numerous map conversions including "Normal Scale of Slopes for Old Large Scale Maps," etc. Units of yards, inches, miles, chains, links, meters, centimeters, kilometers, hours, etc. are used. In very fine condition, it is a most uncommon rule. We find Gunter's instrument offered for sale in a 1907 edition of The Very Best English Goods. The design was first registered in 1896. (10375) $240. |
 |
 |
| Saving a Fortune on Telegraph Charges | Click on any image for a larger view. Scroll to view more items. |
 |
 |
 |
|
THE "CODIGRAPH," French, c. 1910, signed on a plaque "Baveux Frères, Constructeurs, St. Nicolas d'Aliermont, Seine inférieure (France)" and serial numbered 2031. Mounted to a 5-1/8" x 13-3/4" (13 x 35 cm) oak base, the substantial metal cylinder is pierced with five windows for viewing 14 internal cylindrical wheels. These metal wheels are printed, in black and red, with sequences of one or two numbers and letters, and are rotated by six independent knobs at the ends. Some wheels even have their own internal windows. Condition is good, noting some scraping and losses to the paint on the wheels, but with with only minor lossses to any numbers and letters. All seems original (although there is no cover), and it is fully functional. This complex enciphering machine is a rare example of the Ideal Codigraph invented by Charles Durand. It has a fascinating special purpose, driven by early 20th century economics of communication by telegraph. Sending a telegram was quite expensive, and ITU (International Telegraph Union) tarifs charged by the word (up to ten characters for a one-word charge). Numbers were not sent as such by Morse code, but were transmitted as words spelled out in full. The Codigraph transforms large numbers into single pronounceable words ten characters long, with an enormous saving in transmission costs (see Frank Gnegel). A remarkable device. (10425) $4500. |
| Seventeenth Century Mathematics in Brass | Click on any image for a larger view. Scroll to view more items. |
 |
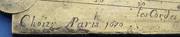 |
|
EARLY FRENCH SECTOR, 1670, signed "Choizy à Paris 1670," and stamped "A. Lee" for a later owner. The brass sector measures 6-3/4" (17 cm) long (closed), the arms engraved with three doubled sector scales on each side: les cordes, les solides, and les métaux, then les parties égales, les plans, et les polygones. Condition is fair to good, noting some pitting, nicks, and stains. Jean Choizy, born in Limoges, is recorded working in Paris from 1649 until his death in 1682. Marcelin finds various instruments by him, including an undated silver sector in the Louvre. And Choizy¹s name appears on a fine surveying compass in the Huelsmann collection (Syndram, 1989, pp. 223-4). A particularly early dated sector, earlier than our 1681 Pouilly (Tesseract Catalogue 91 Item 34). (10385) $1950. |
| By an 18th century Delft Instrument Maker | Click on any image for a larger view. Scroll to view more items. |
 |
 |
|
EARLY DUTCH MATHEMATICAL RULE, second half 18th century, signed "I. Reghter, Delft." This thick brass rule, 14-3/4" (37.5 cm) long, is divided on both sides with a total of six strongly nonlinear scales plus one scale of (Delft?) inches running from 0 to 12, the inches divided respectively into halves, thirds, fourths,..., twelfths (each inch 26.3 mm long). Scales are labeled cryptically "S,N" (1-32, 1-100), "V,R" (1-32, 1-125), and "L,T" (1-32, 1-125). Condition is fine except for several stains to the rule. We do find Reghter's trail in the references -- Zinner lists him as "I. Rechter a Delft," known for a planetarium (in the "Leiden Museum", #A182). King and Millburn describe this as a double-cone planetarium, and refer to Jan or Johannes Reghter (1730 - 1801) of Delft, "a highly skilled maker of compound microscopes, geometrical instruments, and electrical apparatus." Reghter was a published scientist in his own right. He designed and built an atmospheric electrometer which won a prize contest in 1786, and which led to a quarrel when van Breda, who had commissioned Reghter to develop this instrument, took all the credit and the prize (see Zuidervaart, 2006). We have had one other instrument by this maker, an unusual mechanical level with integral scale rule also with the undecoded "V,S,L" scales (Tesseract Catalogue 76, Item 34). (8309) $2950. |
| A Diversity of Slide Rules I | Click on any image for a larger view. Scroll to view more items. |
 |
|
RADIAC SLIDE RULE, FOR NUCLEAR FISSION PRODUCTS, English, mid-20th century, 11-3/4" (30 cm) white plastic with two double-sided slides plus cursor, excellent and fascinating. $595. MINIATURE, probably American, 2nd quarter 20th century, stamped "Buckeye Lamp Division, Cleveland, Ohio," 4-1/2" (11 cm) long plastic over wood, double-sided slide plus cursor, logarithmic and trigonometric scales plus ruler, fine. $120. RICHMOND'S IMPROVED MILK SCALE, English, c. 1915, signed "Daisy Supply Co., Ltd., Park Royal, London, N.W. 10," 12-1/2" (32 cm) long, brass-bound boxwood, scales of Lactodensimeter Reading, Specific Gravity, Temp., Fat, and Total Solids, fine with one chip, rare. $395. COMBINED SLIDE RULE AND RULERS, Japanese, 1961, so dated and signed "Scientific Instruments Co.," Model 1050, 11-5/8" (30 cm) long, plastic laminate over bamboo, double slide, cursor, table to reverse, original leather case, excellent. $275. DICAS HYDROMETRY RULE, English, c. 1815, signed "Dicas Patent Improv¹d by Gill & Co. London," 7-3/8" (19 cm), ivory, slider and scales both sides, Water, Alcohol, Proof, etc., very fine with slide warping. Invented by John Dicas in 1780. SOLD UNUSUAL SOLID IVORY VINTNER¹S SLIDE RULE, English, c. 1815, signed "J.&G. Quin, Patentees," 10" (25 cm), complex with scales both sides including "Sikes¹s Concentrated Strengths," temperature corrections, etc., excellent. (10393) SOLD |
| A Diversity of Slide Rules II | Click on any image for a larger view. Scroll to view more items. |
 |
|
"KEL-CO CLASS CALCULATOR FOR THOROUGHBRED RACE HORSES," American, c. 1975, 10" (25 cm) plastic, with case and instruction booklet, fine but cursor stuck, very complex computations for the winning wager! $295. "CHRONOPOSE EXACT DE CANNEVEL," French, c. early 20th c., 7-1/2" (19 cm), paper over wood with brass, one slide for exposure calculations, the other for actual exposing of photographic test strips, good with wear. $170. THE "UNIQUE" LOG-LOG SLIDE RULE, English, c. 2nd quarter 20th c., 6-3/8" (16 cm), celluloid over mahogany, slide and cursor, trig tables to reverse, good. $150. COMPLEX CIRCULAR SLIDE RULE, American, c. 1940, 4-1/8" (10 cm) diameter, printed on enameled aluminum both sides, with three rotating cursors, excellent. $250. CLASSIC PLASTIC SLIDE RULE, American, c. 1950, copyright by Ecco Co., a diminutive 6-5/8" (17 cm) long, with twin-sided cursor and scales. $95. UNCOMMON KEUFFEL & ESSER SLIDE RULE, American, c. 1920, 10-5/8" (27 cm), plastic laminate to mahogany, table to reverse, beveled linear rule, double-sided slide, cursor with unusual readouts atop and aside for the three logarithmic scales of singles, squares, and cubes, the latter along the side of the rule, very fine with good leather case. $350. THE POST "VERSALOG" RULE, Japanese manufacture, "Hemmi," model 1460 by The Frederick Post Co., 12-1/2" (32 cm), plastic laminate to bamboo, highly complex, double sided, counting 23 scales, with cursors and original leather case, excellent. $330. EARLY FOUR-SLIDE RULE, English, c. 1800, 12" (30 cm), lovely hand stamped boxwood throughout, four sided with four sliders, the latter each with scales or constants or ratios on the inner surfaces, all to enable calculation of numerous mathematical functions and the volume content of partially filled vessels of various shapes, very fine. (10473) $595. |
| Print Your Own -- a Rare Production Plate | Click on any image for a larger view. Scroll to view more items. |
 |
 |
 |
|
BRASS PRODUCTION PLATE FOR SLIDE RULES, American, 1961, signed in the plate "Keuffel & Esser Co., K-12 Prep, K&E 4158." The substantial 12-1/4" x 2-3/4" (31 x 7 cm) brass plate bears in relief the complete highly detailed layout for this single-sided slide rule, with all the divisions, calibrations, and labels. There are nine scales, including those on the slider which here is formed integrally in its zero position on the rule. Condition is excellent. This most rare factory production plate was used for the model 4158 (K12 Prep), which was released in 1961. It was supplanted by the model "68-1892 (K12 Prep)" the following year; consequently it was marketed and sold, but apparently never illustrated in the K&E catalogues. Rare. (10483) SOLD |
| Art and Mathematics in the 17th century | Click on any image for a larger view. Scroll to view more items. |
 |
 |
 |
 |
|
EXCEPTIONAL MATHEMATICAL SECTOR, European, probably German, c. late 17th century. Opening to 17-1/4" (44 cm) this substantial brass sector is constructed with an unusual "sandwich" hinge of concentric disks. The inner disk is hand engraved with a wonderful "rosace" on both sides. The head of each arm is engraved with sinuous floral designs, different on the two sides. There are three different doubled sector scales on each side, including one pair with the planetary symbols of metals. Condition is generally fine noting some nicks and scratches. The decoration on this sector is some of the most appealing we have seen, but identifying the country of origin is difficult. We see considerable similarities to early German sectors, yet the floral images are similar to those on a Blondeau French pearl sizer, and on those on an early Edmund Culpeper English set we had (Tesseract Catalogue G Item 55). A pleasing mystery. (10493) $9500. |
| Sixteen Local Measures Compared, finely subdivided on a Long Scroll | Click on any image for a larger view. Scroll to view more items. |
 |
 |
 |
 |
|
REMARKABLE LINEAR MEASURE COMPARISON SCROLL, German, early 19th century, signed "Leipzig, im Magazin für Industrie und Literatur." A heavy card tube, 9" (23 cm) long, is bound in red paper (simulating Morocco leather), bearing labels for the "Ellenmaass = Tabelle" within, plus identifications of sixteen different linear measures for the ell, mostly local German ones. Included are the Augsburg Elle, the Brabant Elle, the St. Gallen Leinwand, the Russian Archine, and even the French Meter. Rolled within the tube, and wound up by wood handles, is a 42-1/2" (108 cm) long thick paper scroll with sixteen very detailed scales which align with the legends on the tube. The scales run variously from zero up to anywhere from 35 to 64 units, with subdivisions every tenth as well as every twelfth unit. Condition is fine noting some exterior soiling and some small paper losses on the tube ends. According to the labels, this unusual scroll gives comparisons of sixteen of the most common ell measures used in commerce, both German and foreign. The ell was originally defined as the length of the forearm from elbow to tip of middle finger. It evolved into many different regional standard measures, typically about a yard long. A most rare device, the only example we have encountered. (9298) $4500. |
| With Fine 17th c. Decor and Letter Forms | Click on any image for a larger view. Scroll to view more items. |
 |
 |
 |
 |
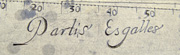 |
|
EARLY FRENCH SECTOR, c. second half 17th century, the substantial brass rule opening on its three-leaf sector hinge to 13-3/8" (34 cm) overall. The hinge is finely engraved with a six-lobed rose on each side, and the near corners of the sector likewise have fine leaf decoration. There are few scales -- only two doubled sector scales per side -- as often the case with the earliest sectors. Exquisitely labeled and with hand-punched numerals, we find "Lignes des Partis Esgalles, Les Plans, Lignes des Cordes, Les Sollides." In fine condition, noting a few stains and with a fine old patina, this is a rare example of early French mathematical instrument. (9309) $2200. |
| Substantial, Precision Logarithmic Slide Rule | Click on any image for a larger view. Scroll to view more items. |
 |
|
UNCOMMON ALL-BRASS SLIDE RULE, French, mid-19th century, unsigned but probably by Richer, stamped on the case "Règle Logarithmique." Measuring a full 17" (43 cm) overall, this substantial rule is made of solid brass, apparently, with a heavy non-tarnishing gray finish. It has a reversible slider, all precision divided with logarithmic "Nomb." scale, and with transcendental trigonometric functions "Sinus," "Tang," and "Caract" scales. Condition is very fine, complete with the original leather covered wood case, the ends notched for use of the calculating rule in place. (9278) $1500. |
| English, Spanish, French Measure Compared | Click on any image for a larger view. Scroll to view more items. |
 |
|
UNUSUAL COMPARISON RULE, English, c. second quarter 19th century, signed "Troughton & Simms, London." This 13-1/2" (34 cm) long brass rule is 5/16" square in cross section, engraved on the four sides with scales of English inches from 0 to 12 by tenths, Spanish inches likewise, old French inches (the old "Pouces du Roy") from 0 to 12 by twelfths, and "Decimetre's" from 0 to 3 by hundreths (i.e., by millimeters). Condition is excellent, complete with its original slightly domed mahogany case. The partnership of Edward Troughton and William Simms commenced in 1826, and was a long-lived manufactory of all manner of optical and mathematical instruments. We have had a number of interesting comparison rules, but none quite like this. It may have assisted in English trade with France and Spain, and was made at a time when the old French inch measure was not yet fully abandoned in favor of the metric system (which was not made mandatory until 1840 -- see item 31 in this catalogue). (9279) SOLD |
| The Metric System Compromised | Click on any image for a larger view. Scroll to view more items. |
 |
 |
|
ENORMOUS METER-LONG MATHEMATICAL SECTOR, French, c. 1820,
signed "Compas (Viret)", and "No. 9." This major instrument
measures 4-1/8" x 20-3/4" x 5/32" (10 x 53 x 0.4 cm) closed,
and opens to a full 39-7/16" (100 cm). It has a three-leaf sector
hinge, and closes on the central steel alignment leaf and the three alignment
pins. One side is divided with a linear scale from 0 to 12 by twelfths,
labeled "Pied Ancien" representing the 18th century standardized
"Pied de Roy" (27.1 mm / inch), plus a double sector scale of
equal parts divided from 0 to 57 by ones. The reverse has (1) a similar
but unlabeled "Foot" scale of 12 inches by twelfths of an inch
(at about 26.8 mm / inch), (2) a linear "Pied Métrique" scale
also running from 0 to 12 by twelfths (and curiously at 27.9 mm / inch),
and (3) a double sector scale of equal parts divided from 0 to 220 by
ones. Condition is fine, noting numerous small nicks and scratches. This
remarkable rule is housed in its softwood case with slide off lid.
The "Pied Métrique" scale on this sector represents a fascinating period in the transition to the metric system in France. An inch of 27.9 mm gives a foot of approximately 335 mm (actually intended to be 333-1/3 mm), and thus a meter of exactly 3 feet. This was part of the "mesures usuelles" introduced by Napoleon in 1812, and finally abolished in 1839. The formal metric system had been gradually introduced into France, département by département (Paris being first), between 1795 and 1800. It was poorly understood by the populace, unpopular, and little used in local trade. As a compromise, Napoleon introduced this sort of "metric" system based on the old measures. A meter thus equaled one yard of three traditional feet, the liter was subdivided as a quart, the kilogram was specified as exactly two pounds, etc. It was a confusing journey into the eventual acceptance of the greatly simplified true metric system. The engraved word "Viret" in parentheses is something of a puzzle, but probably indicates the maker of this grand sector. A clockmaker by this name is indeed listed in Paris directories during the 1820's, and a splendid gilt clock by him is known. (9366) $4950. |
 |
 |
| Rare Multifunction Slide Rule for Chemistry | Click on any image for a larger view. Scroll to view more items. |
 |
|
CHEMICAL ENGINEERING SLIDE RULE, Japanese, c. 1960, signed "Hemmi, Japan, No. 257." The 12-1/2" (32 cm) long rule is made of laminate over bamboo, metal bound, and fitted with double-sided sliding glass cursor. The two sides of rule and slider are divided with a total of 23 scales, including gauge marks for determination of atomic and molecular weights, temperature, conversion scales, pressure unit conversions, molar / weight / volume fractions, adiabatic compression and expansion, etc. In addition there are the standard scales of multiplication, roots, logarithms, exponents, etc. The outfit is in near new condition, complete with instruction manual and leather case. The Hemmi Slide Rule Company was established in 1895 (first as Henmi Jirou & Co.) They became a major manufacturer of both standard and specialized slide rules, introducing the model 257 in 1954. But within 10 years the introduction of electronic calculators initiated the precipitous decline in slide rule manufacture, and the Hemmi company eventually turned to electronics. (7316) $950. |
 |
| A Most Rare Patented Calculator | Click on any image for a larger view. Scroll to view more items. |
 |
|
THE "CALCULATEUR DIDELIN," French, c. last quarter 19th century, "Brevete France S.G.D.G. et Etranger." The 19-1/2" x 8-1/2" x 2-1/2" (50 x 22 x 6 cm) softwood case, with hinged lid and sides, contains a system of five lithographed tin rollers, plus a hinged overlay plate with a total of 150 (!) windows opened and closed by 30 independent shutter slides. The rotating tubes (for units, tens, hundreds, thousands, and ten-thousands) are printed with interest due for 30 different percentage rates (from 0.25% up to 9%). Condition is fine throughout noting a little wear and soiling. It is an intriguing and quite rare specialized calculator; we find no example in the published catalogues of the collection in the Science Museum in London, and but one in the Musee des Arts et Metiers, that one given to the Museum by Monsieur Didelin himself in 1892. (7337) $3500. |
 |
| Patented French Calculator | Click on any image for a larger view. Scroll to view more items. |
 |
| Musical Scale on an Early Sector | Click on any image for a larger view. Scroll to view more items. |
 |
|
A MUSICAL SECTOR, German or Italian, c. late 17th century, made of brass, reverse tapered in thickness, opening from 7-1/2" to 14-1/8" (19 to 36 cm). One side is finely divided with twin sector scales of equal parts (each scale divided twice 0(1)100; i.e., from 0 to 100 by ones), of "Lin Recta" 15(1)2, of "Lin 'square'" 0(1)60(5)90, and of a wonderful musical scale "fi, G, G-is, a, b, h, C, C-is, D, D-is, E, f." The other has twin sector scales of "Lin Cub" 1(1)50(5)120 and "Lin Circul" 60(5)45(1)6, noting a couple of tiny terminal fleur-de-lis marks . Condition is good with general surface wear. This interesting sector has standard scales for computing distances, areas, etc. But it also has a musical scale of 12 notes, spaced nonlinearly and representing the differences in pitch. It is specifically German nomenclature, distinguished by the "-is" abbreviation sign (engraved here somewhat like the Greek beta) meaning "sharp", the "b" for B-flat, and the zigzag-h for B-natural (Jeffrey Dean, 2012; and see W. Apel, 1949, The Notation of Polyphonic Music, 900-1600). Such a musical scale can have many uses in the design and construction of instruments, for example calculation of lengths of lute strings or organ pipes, of string gauges or tensions, or even of bell diameters. The only other musical sector scales we have found are on very large German sectors (e.g. see R. de Pecker, 2007, and a particularly fine example at Oxford). (9395) SOLD |
 |
| "Arithmetical Not Zoological" | Click on any image for a larger view. Scroll to view more items. |
 |
 |
|
FIRST FORM OF WEBB'S ADDER, American, c.1875, signed "C.H. Webb, N.Y., 'The Adder,' Patd. March 10th, 1868," #C671. Made of sheet brass on mahogany, 6-3/4" (17 cm) overall, this is the uncommonly found early form of Webb's "two-wheeled velocipede of figures." Described in detail by Kidwell in Rittenhouse (1, 12), it was succeeded by Webb's popular all-metal version. This is a good example of this American calculating instrument, in fine condition, with photocopies of Webb's instructions and glorious testimonials. The New York Times of 2 Jan. 1869 headlines "'The Adder' -- Arithmetical Not Zoological." And from Inventors and Manufacturers'Gazette of the same month, "This 'Adder' can easily be worked in a room where a dozen persons are engaged in conversation, and the operator himself can talk during the adding process without fear of blunders." Webb himself seems to have been a man of many talents. Under the pen name "John Paul" he was the "wise and witty New York correspondent" to the Springfield, Massachusetts Republican; he authored Wickedest Woman in New York, and was the playwright for numerous burlesque performances. (9303) $975. |
 |
 |
| Specialized "Napier" Rods from The Netherlands | Click on any image for a larger view. Scroll to view more items. |
 |
|
SPECIALIZED CALCULATING RODS -- "NAPIER'S BONES" FOR SIZE AND WEIGHT CONVERSIONS, Dutch, c. 1800, with the partial trade label of "Dirk Van Den Bosch," mathematical instrument maker of Rotterdam. The fine mahogany case contains this complete set of 20 four-sided, 8-3/8" (21 cm) long, boxwood rods. Each rod is numbered on top with an integer from 0 to 9, and punched on each face with four sets of columns of nine numbers, each column headed by different lettered abbreviations. The latter are identified on a label in the case, being RV (Rheinland foot), AV (Amsterdam foot), HE (The Hague ell), HTP (Holland troy pound), AP (Amsterdam pound), NE (Netherlands ell), and NP (Netherlands pound). Further abbreviations have these letters preceded by V (for squares) or K (for cubes). In addition to the printed trade label and table of ratios (Verhoudingen) in the box, there is an old manuscript explanation written (in Dutch) by an early user. This note refers to van Swinden, the famous Dutch mathematician and physicist who wrote a major work on weights and measures, and was instrumental in bringing the metric system to the Netherlands. Condition is excellent noting some rods warped, and an old crack in the case lid. This is the first such set we have encountered. In using it we find, for example, that one side of the "1" rod has columns for RV, NE, HE, and NE. The first column gives, to nine decimal places, the number of Rheinland feet in one Netherlands ell; the second column the reciprocal; the third the number of The Hague ells in one Netherlands ell; the fourth the reciprocal of that. The same face on the "2" rod has the same entries doubled, and so on to the "9" rod. Assembling a group of rods, and adding along the diagonals as with Napier's rods, we find directly how many of one unit are in any very large number of the other unit of length, or weight. With the "V" and "K" scales we can do this direct conversion for areas and for volumes, respectively. The maker / retailer of this ingenious set is not found in the standard references. (9352) $9500. |
 |
| Calculator in Your Pocket, c. 1900 | Click on any image for a larger view. Scroll to view more items. |
 |
|
THE CALCULIMETRE CHARPENTIER, French, c.1900, signed "Calculimetre, G. Charpentier, Brevete S.G.D.G." The 2-3/8" (6 cm) diameter calculator is made of nickel silver and brass, divided with logarithmic, square root, tangent and sine scales on both sides, the suspension affixed to twin cursors and a frontal circular scale. A milled edge allows one to rotate the main body against this suspension assembly. Condition is fine, the surface somewhat cleaned and scratched. The Charpentier calculator, a fine pocket slide rule, is analogous to the Mannheim design but with circular scales. It was covered by a French patent, and by a British one in 1882, and was listed in American Keuffel & Esser catalogues from 1895 up to 1927, and in Dietzgen catalogues (see Otnes, 1991). Despite this, surviving examples are relatively uncommon; here we are able to offer a good French one, complete with photocopies of instructions and of the original French patent papers. (9331) $1250. |
| From the Thirty Year's War | Click on any image for a larger view. Scroll to view more items. |
 |
 |
 |
|
SEVENTEENTH CENTURY GUNNERY GAUGE, German or Austrian, 1629, boldly engraved "Anno 1629." Rectangular in cross section, and tapered, the brass rule measures 13-1/2" (34 cm) long overall, including its cast and soldered double-sided bust handle. Each face of the rule is hand engraved, one with a scale of inches (labeled "Zol") from 0 to 12, each inch subdivided into the corresponding integral number of parts (e.g., the eleventh inch is divided into 11 equal parts!) Each inch measures approximately 24.1 mm, and is thus consistent with the local foot measure in a number of German city states (see Gilliland, SIS Bulletin 20, for an overview). The other three sides are divided nonlinearly, giving the weight of a cannonball of the measured bore diameter, for "Eisen Kugel" (Iron Balls) from 0 to 125 "Pfunt" (pounds), for lead balls (also over the range 0 to 125), and for stone balls (0 to 60 pounds). Condition is very fine. Related gauges, one even with a bust, exist in the Dresden princely collections, illustrated in Grotzsch & Karpinski (1978, fig. 140). The present one dates from the Thirty Year's War (1618 -1648), which raged throughout Europe and devastated Germany. It is intriguing to seek an identification of the bust, assuming it is specific, but so far this is too speculative. What we do have is a wonderful dated survival from the early 17th century. (8377) $19,500. |
| Complex Scales by Engineer to Brunel | Click on any image for a larger view. Scroll to view more items. |
 |
 |
|
METFORD'S QUADRUPLE ENGINEERS SCALES IN IVORY, English, late 19th century, signed "Metfords Engineers Pocket Scales" and "Hudson & Kearns, London." The four ivory rules are each 6-1/2" (17 cm) long, of triangular cross section, and divided on all three sides with scales, constants, measured values, equations, etc. There are simple linear charting scales very finely divided (e.g., "6 inches to a mile"); relationships in triangles ("Hypoth= Base x Sec Angle at Base"); "Ordnance Scale;" expansion measurements for mercury, for glass tubes, for steel rods, etc; specific gravity of palladium, aluminum, etc; the logarithm of the force of gravity; the one-hundredth of a second of arc at the equator, measured in English feet; etc. We count 17 divided scales and numerous useful facts. Cryptic abbreviations on the ends of each rule form a table of contents. Condition is excellent except for a small chip at one end of one rule. The original leather bound case is present, lacking its end piece. The inventor was presumably William Ellis Metford (1824 - 1899), a dedicated engineer who worked under Brunel for a time, and who is known for his improved surveying theodolite (see his high quality miniature theodolite "The Metford Theodolite with Repeating Circle," Tesseract Catalogue 64 Item 23.) One example of "Metford's Double Set of Ivory Pocket Scales suitable for Civil Engineers, Architects, and Land Surveyors" is presumably in the Science Museum -- we find it listed in the Catalogue of the Educational Division of the South Kensington Museum (1867). That set was signed by Pastorelli & Co.; ours by Hudson & Kearns, known especially as publishers in late Victorian England. A rare example of this complex set. (8357) $3950. |
 |
 |
| A Splendid Calculating Rule in Silver | Click on any image for a larger view. Scroll to view more items. |
| A Complex Circular Calculator | Click on any image for a larger view. Scroll to view more items. |
| The Power of Radioactivity | Click on any image for a larger view. Scroll to view more items. |
| Astronomy |
| Microscopy |
| Dialling |
| Navigation |
| Demonstration & Experimentation |
| Calculation |
| Medical |
| Specials |
| Books New and Old |
| Tesseract Catalogues |